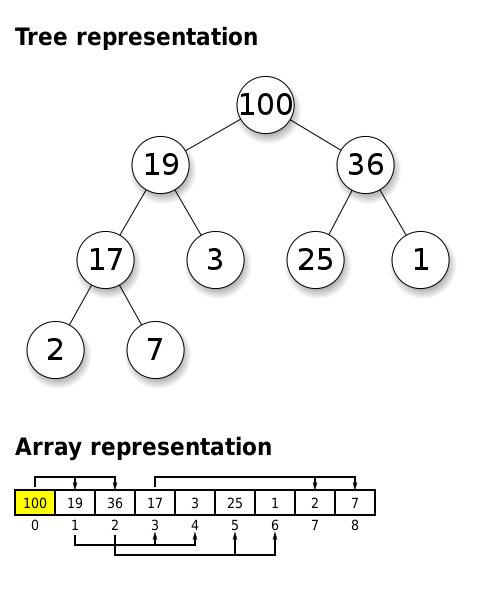
힙(Heap)
힙은 최대값 혹은 최소값을 매우 빠르게 찾아내기 위한 자료구조로, 완전이진트리를 기반으로 한다.
힙에는 최대힙과 최소힙 두 가지로 나뉘는데, 최대힙은 부모 노드가 자식 노드보다 항상 커야 하고, 최소힙은 부모 노드가 자식 노드보다 반드시 작아야 한다.
대소 관계는 부모와 자식 노드 간에서만 성립해야 하며, 형제 노드끼리는 성립하지 않는다.
힙에서는 가장 높은 우선순위를 가진 값(가장 큰 값, 혹은 가장 작은 값)이 루트 노드로 오는 특징이 있다.
이러한 특징을 이용해 우선순위 큐로 사용하기에 용이하다.
구현
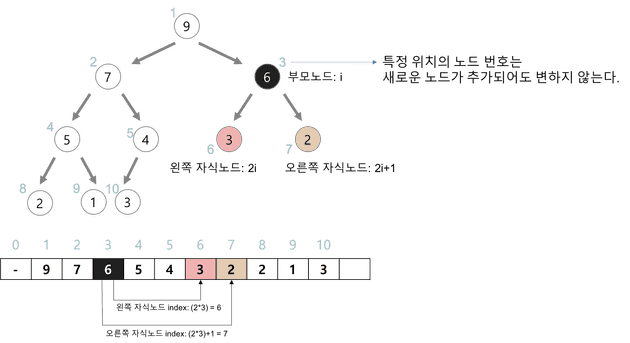
힙은 보통 배열을 이용하여 구현된다. 기반이 완전이진트리이기 때문에 중간에 빈 공간이 없어 배열로 구현하기 용이하다.
루트 노드(인덱스 0)를 제외한 임의의 노드의 인덱스 i에 대해, 부모 노드의 인덱스는 항상 i/2가 성립하고 왼쪽 자식 노드의 인덱스는 2*i, 오른쪽 자식 노드의 인덱스는 2i + 1가 성립한다.
힙 재구조화 (Heapify)
삽입
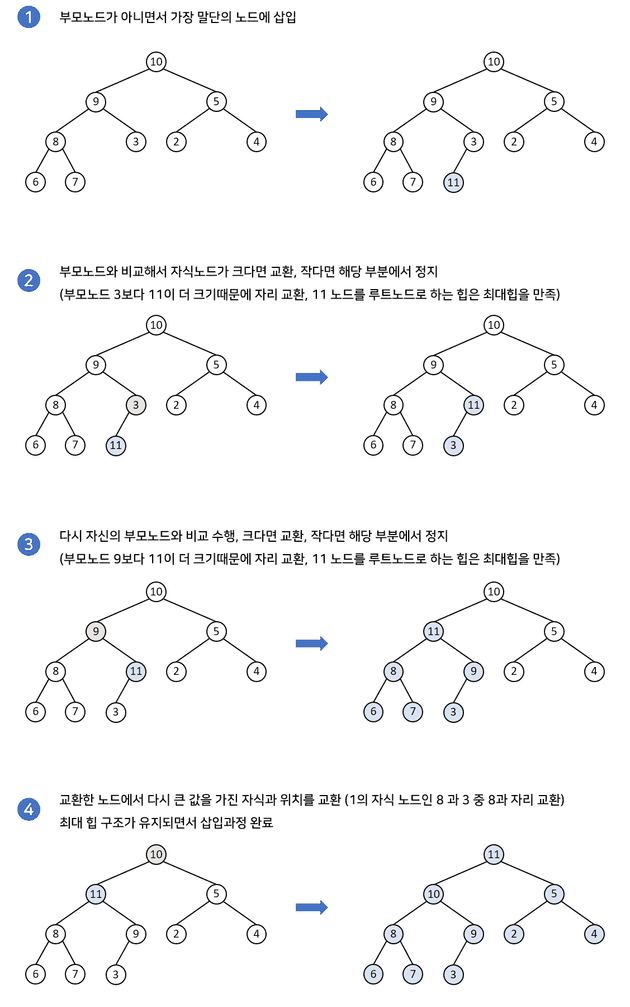
힙에 새로운 값을 삽입하면 다음 과정이 일어난다.
- 저장할 수 있는 마지막 인덱스 위치에 값을 추가한다.
- 해당 값의 부모 노드와 대소를 비교한다. 이때 새로 추가된 값이 우선 순위가 더 높은 경우 부모 노드와 위치를 바꾼다.
- 2번 과정을 부모 노드보다 우선순위가 더 낮거나, 루트 노드에 도달하는 순간까지 반복한다.
완전이진트리의 높이를 h라고 했을 때, 걸리는 시간 복잡도는 O(logh) 이다.
삭제
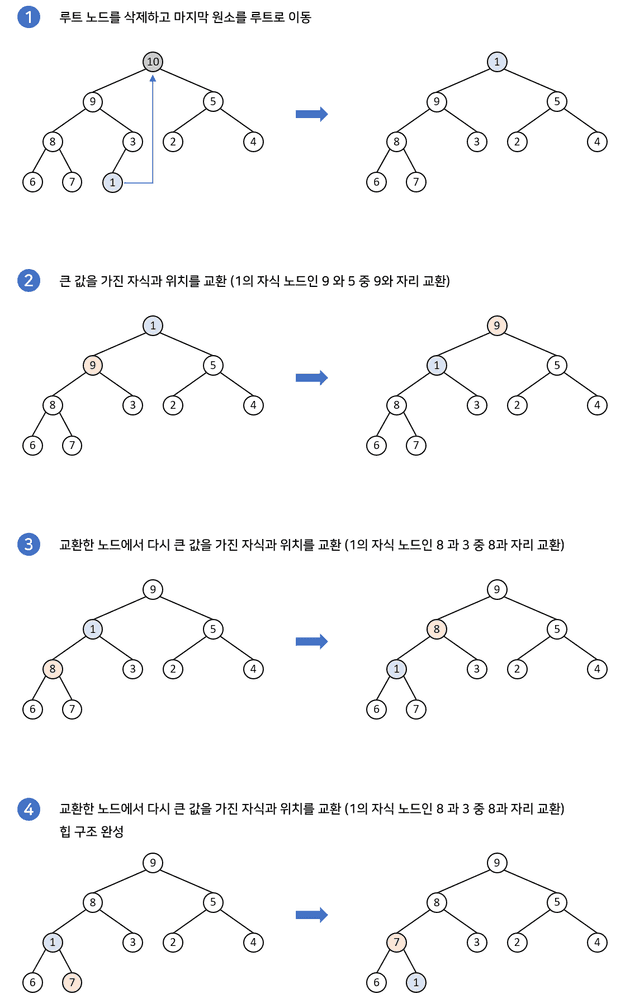
루트 노드의 값이 추출될 경우 다음 과정이 일어난다.
- 가장 마지막 인덱스 위치에 있는 값을 루트 노드로 이동한다.
- 루트 노드의 두 자식 노드를 비교해서 더 우선순위가 높은 값과 자리를 바꾼다.
- 그 다음 바뀐 자리에서의 두 자식 노드를 비교해서 더 우선순위가 높은 값과 자리를 바꾼다.
- 위 과정을 더이상 바꿀 수 없거나 바꾸지 않아도 될 때까지 반복한다.
삭제도 마찬가지로 트리의 높이를 h라고 했을 때, 소요되는 시간은 O(logh) 이다.
힙 만들기(Build Heap)
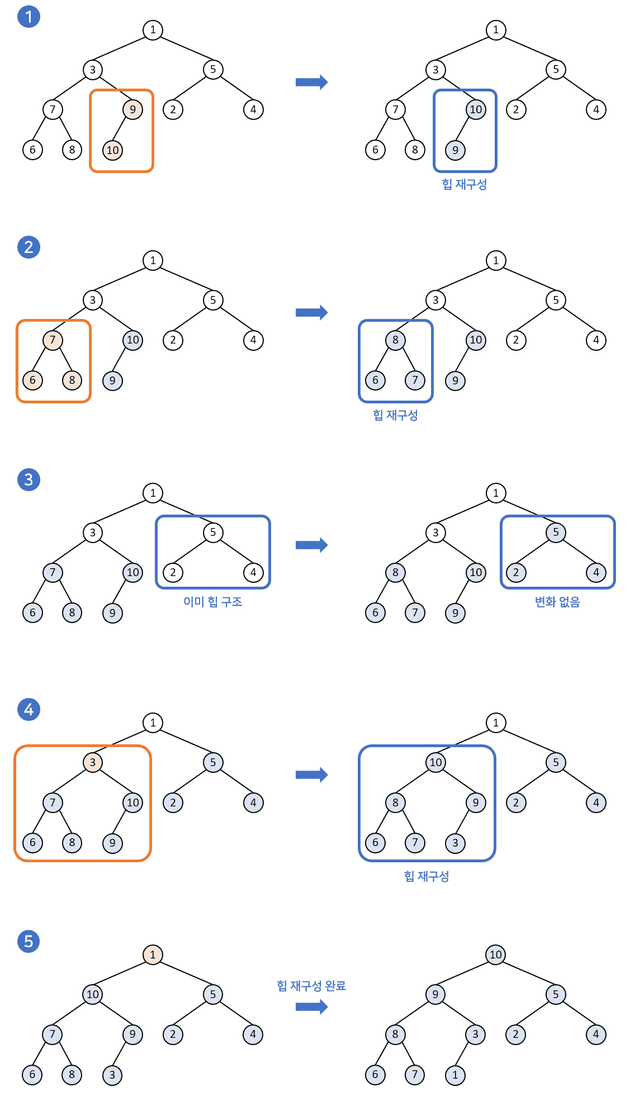
만약 값들이 임의의 순서를 가진 배열을 힙으로 만드려면 어떻게 해야 할까? 시간 복잡도는 어떻게 될까?
이때는 뒤에서부터 한 묶음의 부모-자식 관계를 모두 보면서, 힙을 만들면 된다.
다르게 말하면 분할정복 방식으로 힙을 완성시킨다고 표현할 수도 있겠다.
과정은 다음과 같다.
Python에서 Heap 사용하기
Python에서는 Heap을 사용하기 위해서는 heapq 모듈1을 사용한다.